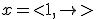
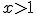
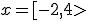
Wiskunde. Voor de één een hel, voor de ander een deel van het leven en een "eitje". Hier kun je in ieder geval terecht met al je vragen. Gelijkbenige driehoeken, de stelling van Pythagoras (dooie Griek), wiskunde A,B,C en D: alles is mogelijk. Let wel: je krijgt ondersteuning en uitleg maar het is geen huiswerkservice dus pasklare antwoorden worden niet gegeven......

Weggehaald...

Bewerkt: 10 maart 200817 jaren door K.O.

Wiskunde D is volgens sommige mensen de zwaarste wiskunde die je kunt kiezen, maar in de praktijk verschilt dat heel erg per persoon. Ikzelf vind Wiskunde D niet moeilijker dan B, ik ken mensen die dat wel vinden en ik ken mensen die Wiskunde D juist makkelijk vinden.

Welk boek heb jij voor wiskunde?

Ik heb ook wiskunde B en over een week start wiskunde D op onze school (7 uur wiskunde is de week ).

Wij hebben het boek Getal en ruimte. Iemand had bij wiskunde b ooit gezegt dat hij wis D er makkelijk uit vond zien ofzo en toen zij onze lerares dat het eerste boek makkelijk is en wat we in 5 de klas krijgen veel moeilijker.

Bewerkt: 22 januari 200817 jaren door Gta-killer

Hallo iedereen,

Voor mensen die Getal en Ruimte gebruiken, goed nieuws!

Hier staan alle uitwerkingen: http://home.hccnet.nl/t.amerongen/Uitwerki...oofdstukken.htm

Er zijn nog meer sites maar dit is volgens mij de beste.

Van de nieuwe uitgave zou ik niet weten hoe het zit, maar mensen die nog in de oude 2e fase zitten hebben hier in ieder geval heel veel aan. Altijd handig, want die standaard antwoordenboekjes van die methode zijn maar prut, aan alleen een antwoord heb je niks...

Hoi, ik heb morgen proefwerk van Wiskunde. Ik moet de formules onthouden van: Omtrek, inhoud, inhoud circel.

Hoe leer ik deze goed uit mij hoofd, of misschien ezelsbruggetjes ?

Hoi, ik heb morgen proefwerk van Wiskunde. Ik moet de formules onthouden van: Omtrek, inhoud, inhoud circel.

Hoe leer ik deze goed uit mij hoofd, of misschien ezelsbruggetjes ?

Mag je gebruik maken van een grafische rekenmachine? Waar je dus ook informatie in op kan slaan?

Anders zou ik het gewoon stampen, want echt ezelsbrugetjes weet ik er niet voor. Misschien dat je hier (ezelsbruggetjes-site) nog iets tegenkomt.

Edit: zoals deze:

Cirkel: omtrek of oppervlakte?

De omtrek is 2.pi.r, de oppervlakte is pi.r kwadraat. Als er 1 r in voor komt, is het dus in meters en dus lengte. Als er r-kwadraat in voor komt, is het vierkante meters, dus oppervlakte!

Ingezonden door: Rob

Gaat het trouwens om een bol of een cirkel? Is het 2D of driedimensionaal? Een cirkel heeft namelijk geen inhoud en voor een bol gelden andere formules.

Bewerkt: 28 januari 200817 jaren door K.O.

Hoi, ik heb morgen proefwerk van Wiskunde. Ik moet de formules onthouden van: Omtrek, inhoud, inhoud circel.

Hoe leer ik deze goed uit mij hoofd, of misschien ezelsbruggetjes ?

Mag je gebruik maken van een grafische rekenmachine? Waar je dus ook informatie in op kan slaan?

Anders zou ik het gewoon stampen, want echt ezelsbrugetjes weet ik er niet voor. Misschien dat je hier (ezelsbruggetjes-site) nog iets tegenkomt.

Nee, kan er jammer genoeg niks op opslaan. Toch bedankt

Omtrek was toch 'pi x diameter' , en inhoud ´pi x straal²´.

Omtrek was toch 'pi x diameter' , en inhoud ´pi x straal²´.

Ik geloof dat je die laatste formule ook nog moet vermenigvuldigen met de lengte, maar pin me daar niet op vast.

Je rekent daar namelijk de opp van "een schijfje" mee uit zegmaar, zal even een voorbeeld proberen te geven.

Omtrek was toch 'pi x diameter' , en inhoud ´pi x straal²´.

Ik geloof dat je die laatste formule ook nog moet vermenigvuldigen met de lengte, maar pin me daar niet op vast.

Je rekent daar namelijk de opp van "een schijfje" mee uit zegmaar, zal even een voorbeeld proberen te geven.

<*afbeelding*>

Ging het niet om een cirkel/bol? Een cilinder (of koker zoals je het noemt) is een heel ander figuur. Ik ben via Google dit tegengekomen. Dit zijn de formules voor omtrek/oppervlakte/inhoud voor een cirkel/bol/cilinder:

Ik zit met een wiskunde probleempje (en neem aan dat een dubbelpost in dit geval wel geoorloofd is?)

Stel je hebt 5 knikkers. Deze knikkers verdeel je over een n-aantal bakjes. Bij 1 bakje hebt je maar 1 mogelijkheid. Bij 2 bakjes heb je 6 mogelijkheden:

0|5, 1|4, 2|3, 3|2, 4|1 en 5|0

Bij 3 bakjes 21 en zo verder. Wat gevraagd wordt, is de som van het aantal mogelijkheden bij 1 tot en met 500 bakjes.

Is dit te bepalen met een recursie-/rangnummerformule? Ik zie echter niet direct een verband in deze rij:

u(n) = 1 , 6 , 21 , 56 , 126 , 252 , 462 , 792 , 1287

of in deze somrij:

s(n) = 1 , 7 , 28 , 84 , 210 , 462 , 924 , 1716 , 3003

Iemand die een idee heeft?

(Waarom wordt ik nooit geholpen met dit soort dingen!? Ik bedoel, ik vroeg dit op 10-03 en inmiddels zijn we dik een maand verder, 10-04. Er zijn toch wel mensen die dit weten?)

Bewerkt: 12 april 200817 jaren door K.O.

ik snap iets niet van onbinden in factoren

kan mij iemand daar meer uitleg over heven

zonder gemeenschapelijke factor

vb Xtot de 2de min ytot de 2de

wat bekomt dat dan

ik snap iets niet van onbinden in factoren

kan mij iemand daar meer uitleg over heven

zonder gemeenschapelijke factor

vb Xtot de 2de min ytot de 2de

wat bekomt dat dan

Je bedoelt x² - y²? Dit wordt gewoon (x - y) . (x + y) (de . is een maalteken, voor de duidelijkheid) Een ander voorbeeld, wat je natuurlijk ook zonder ontbinden in factoren kan oplossen, maar ter verduidelijking: 16 - 9 = (4 - 3) . (4 + 3) = 1 . 7 = 7.

Voor een opdracht bij Wiskunde moet ik p³ - 3pq ontbinden in factoren. Ik kom er ff niet uit. Ik zat zelf te denken aan p(p²-3q), maar om de een of andere reden lijkt me dat gewoon fout. Kan iemand even het juiste antwoord geven a.u.b.? (uitleg over ontbinden in factoren heb ik voor de rest niet nodig, aangezien ik alle andere opdrachten waarin je moest ontbinden probleemloos kon maken).

Alvast bedankt.

@ hieronder: Zeker weten ja? Oké, bedankt, dan ga ik er maar uit dat het zo goed is.

Bewerkt: 13 april 200817 jaren door BaasB

Voor een opdracht bij Wiskunde moet ik p³ - 3pq ontbinden in factoren. Ik kom er ff niet uit. Ik zat zelf te denken aan p(p²-3q), maar om de een of andere reden lijkt me dat gewoon fout. Kan iemand even het juiste antwoord geven a.u.b.? (uitleg over ontbinden in factoren heb ik voor de rest niet nodig, aangezien ik alle andere opdrachten waarin je moest ontbinden probleemloos kon maken).

Alvast bedankt.

Hoezo zou dat niet kunnen? Voor zover ik er verstand van heb is het zo prima.

Voor een opdracht bij Wiskunde moet ik p³ - 3pq ontbinden in factoren. Ik kom er ff niet uit. Ik zat zelf te denken aan p(p²-3q), maar om de een of andere reden lijkt me dat gewoon fout. Kan iemand even het juiste antwoord geven a.u.b.? (uitleg over ontbinden in factoren heb ik voor de rest niet nodig, aangezien ik alle andere opdrachten waarin je moest ontbinden probleemloos kon maken).

Alvast bedankt.

@ hieronder: Zeker weten ja? Oké, bedankt, dan ga ik er maar uit dat het zo goed is.

Ik bevestig 'm ook >: D